Firstly ,what is a matrix?
A Matrix is a rectangular array of numbers arranged in rows and
columns .
Matrices can contain complex numbers but they are designed to keep the data as simple and small as possible .The image to the right has two examples of matrices.
Now let's go into the uses of matrix.
Use of matrix in the business
field.
Consider a company with
several outlets selling several different products, a matrix provides a concise
way of keeping track of stock.
|
Outlet
|
Milo
|
Milk
|
Bar soap
|
Bath gel
|
|
|
|
|
|
|
|
Ghana
|
110
|
130
|
170
|
180
|
|
Nigeria
|
290
|
105
|
145
|
125
|
|
Togo
|
170
|
90
|
140
|
160
|
|
Benin
|
145
|
115
|
200
|
195
|
Reading across a row of
the matrix, the firm(Nestle) can determine the level of stock in any of its
outlets.
By reading down
the column, the firm can determine the stock of any of it’s products.
Use of matrix
in graph theory.
The adjacency
matrix of a finite graph is a basic notion of the graph theory.
Use of matrix
in the field of computer science.
It is used in
computer graphics; the first model of quantum mechanics also known as matrix
mechanics.
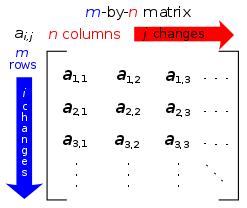
To our left ,we can see the format of a matrix .
'm' represents the rows and 'n' the columns .
'i' represents the number of rows and 'j' the number of columns .
This number of rows and columns that a matrix has is known as the order of matrix .
Now lets get to types of matrix .
The following are the types of matrices which are commonly used to represent data :
1. Row matrix : This matrix has only one row and 'n' number of columns .2. Column matrix : This matrix has only one column and 'm' number of rows .
3. Zero matrix or the null matrix : This one is called as such because the elements it would contain are equal to zero (0) .
4. Square matrix : The square matrix has equal number of rows and columns ,pretty obvious why it is named 'square matrix' .It simply means that 'm' = 'n' .
5. Diagonal matrix : It is a square matrix in which the non diagonal elements are equal to zero .
6. Scalar matrix : It is a diagonal matrix in which all the diagonal elements are equal .
7. Unit matrix or the identity matrix : A square matrix with ones (1) on the diagonal and zeros (0) elsewhere .This matrix is to be denoted by 'I' .
8. Upper Triangular Matrix : A matrix in which the elements below the main diagonal are equal to zero '0' .
9. Lower Triangular Matrix : A matrix in which the elements above the main diagonal are equal to zero '0' .
No comments:
Post a Comment